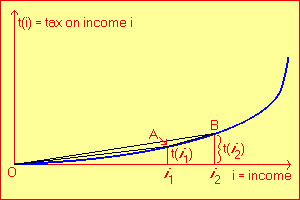
At an income of i1, the total tax is t(i1). The average tax rate is t(i1) / i1, which would typically be expressed as a percentage. This rate is shown geometrically as the slope of line segment OA. Similarly, at income i2 the total tax is t(i2) and the average tax rate is t(i2) / i2, indicated by the slope of segment OB. Because i2 > i1, the average tax rate at i2 must exceed the average rate at i1 (by the definition of a convex tax structure), and it can be seen that the slope of OB is greater (that is, steeper) than the slope of OA. The marginal tax rate associated with an income increase from i1 to i2 is represented by the slope of segment AB. It should be clear from inspection that this slope must be greater than the slope of either segment OA or segment OB; an algebraic proof is also provided (Open Details window). Convex Income-Tax Structure

In summary, the so-called "progressive" tax structure, which is the most widely favored form of income tax, is precisely the form most destructive to economic prosperity.      Next page
Previous pagePrevious Open Review window